Effect of Instructions on a Two-choice Probability Learning Task
Sandra V. Wakcher1
California State University, Fullerton
Abstract
The effect of instructions on a two-choice probability learning task was investigated. The present study was conducted via the World Wide Web and extends on Birnbaum’s (in press) Web-based probability learning experiment. Whereas Birnbaum used a binary abstract task, the present study used a horse race scenario in which participants predicted the winner in a series of races between two horses. Instructions served as independent variables that were manipulated between participants. It was predicted that giving participants the optimal strategy to use, probability of events, and a money scenario would increase the percentage of correct predictions and reduce the use of the probability matching strategy, which is to match choices to probability of events. Results showed that giving participants the strategy and probability of events improved performance on the probability learning task. However, instruction effects were not significant, and the money scenario did not appear to improve performance.
Effect of Instructions on a Two-choice Probability Learning Task
We are required to make decisions daily, from simple ones like what to have for breakfast to important, more complex, ones like what graduate program to attend. According to economic theory, people are fundamentally rational and make decisions that maximize their benefits (Herrnstein, 1990). For instance, we would choose to eat breakfast foods that we enjoy, will satisfy our appetite, and will not harm us. Although humans are, for the most part, hedonistic beings, this does not mean that we necessarily know how to make decisions that will maximize our gains and minimize our losses. Indeed, probability learning experiments have shown that people do not always make the most favorable decisions (Birnbaum, in press; Brehmer & Kuylenstierna, 1980; Erev, Bereby-Meyer, & Roth, 1999; Gal & Baron, 1996; Nies, 1962; Tversky & Edwards, 1966).
In probability learning experiments, judges are asked to choose between two or more events that have different chances of occurring. For example, a judge may be asked to predict the random draw of a card that has a 23% chance of being a face card and a 77% chance of being a number card. After each decision, judges receive feedback letting them know if they were correct. In this type of task, individuals could maximize their successes by always choosing the more likely event (e.g., the number card). Nevertheless, individuals do not typically use this strategy. Instead, they tend to match the probability of their choices to the probability that the event actually occurs.
Tversky and Edwards (1966) found that judges probability matched when they were asked to predict which of two lights was going to turn on next. For example, if the left light turned on 70% of the time, judges would predict 70% for the left light and 30% for the right light. Because judges’ predictions are independent of the lights actually turning on, matching the probabilities of the events would lead the judges to correctly predict the left light (.70) (.70) = .49 of the time and the right light (.30) (.30) = .09 of the time. Thus, this type of decision-making is suboptimal and has a success rate of .49 + .09 = .58. The optimal strategy would be consistently choosing the left light, which would lead to a success rate of 70%. However, Tversky and Edwards found that judges reported that the "best" strategy to use for this type of task is to observe the frequencies of each light (i.e., calculating reinforcements) and then make predictions that match those frequencies, which is what most of the participants did.
In a more recent study, Birnbaum (in press) also found evidence for probability matching in both laboratory and Web-based studies. Judges were asked to predict which of two abstract events (R1 or R2) would happen next and were given feedback to whether they were right or wrong on each trial. Birnbaum found that judges did not consistently choose the more likely event. Instead, they matched their probability of choosing R1 or R2 to the probability that each event actually occurred.
The suboptimal "matching" behavior found in probability learning experiments may be explained by the law of effect, which states that behavior that is reinforced will be repeated more than behavior that is not (Herrnstein, 1990). The feedback judges receive after each prediction becomes the probabilistic reinforcement that shapes their future choices and leads them to probability matching.
Although laboratory decision-making may seem trivial, probability matching can have serious consequences in real-life situations. For example, people may use this type of strategy when driving or making medical diagnosis, which could have life or death consequences. It is therefore important to find what can be done to improve individuals’ decision-making strategies.
Nies (1962) manipulated the instructions that were presented to judges to see if people could profit by instruction. Judges were divided into three groups and were instructed to predict whether a marble rolling out of a box would be red or blue and to get as many correct predictions as possible. Two of the three groups were given additional instructions: one group was told that there were 100 marbles in the box and that 70 were red and 30 were blue, and a second group was told that the marbles roll out in a pattern. The third group did not receive additional instructions. Nies found that the group that was told the proportion of red and blue marbles achieved a higher percentage correct than the other two groups. Only 4% of the judges, however, used the optimal strategy of always predicting the more likely marble.
Because individuals presumably make choices based on reinforcements, changing the strength of the reinforcement may affect performance. Bereby-Meyer and Erev (as cited in Erev et al., 1999) tested this assumption by asking judges to guess which of two abstract events will happen next (L or H) and offering different payoffs for wrong and right answers. The researchers found that when judges gained four points for correct answers and lost nothing for wrong answers, they chose the more likely event (H) less often than when judges lost points for wrong answers. A follow-up study by Bereby-Myer and Erev (as cited in Erev et al., 1999) yielded similar results: judges perform better when losses are involved. Thus, judges may be more motivated to perform when threatened by losses.
Overall, probability learning experiments have yielded mixed results as to what improves performance. The present study will extend on Birnbaum’s (in press) Web-based probability learning experiment by adding and manipulating instructions that were theorized might improve judges’ performance. Whereas Birnbaum used abstract events, the present study will use a horse race scenario in which participants were asked to predict the winner in a series of races between the same two horses. To see if different scenarios have an effect on probability learning, the abstract task in Birnbaum’s study was also used for comparison.
Predictions made for this experiment are based on the assumption that people want to maximize their successes and minimize their losses and will therefore use available information to their advantage. In this experiment, "success" means the correct prediction of an event. It is predicted that telling participants the best strategy to use (i.e., always choose the more likely alternative) will reduce probability matching, and therefore increase the percentage of correct predictions. Furthermore, it is theorized that telling participants the probability of events will cause them to choose the more likely event more often; thus yielding a greater percentage of correct predictions.
Nies (1962) found that probability information achieved a higher percentage of correct responses; however, only 4% of judges used the best strategy of always choosing the more likely alternative. Although judges know probability of events, they may not know how to apply this knowledge to the task at hand. For instance, if judges do not realize that events are independent of one another, they may continue to match their choices to the probability of events (Gal & Baron, 1996). Therefore, it is theorized that when strategy and probability instructions are presented together judges will achieve a higher percentage of correct predictions than when the probability instruction is presented without the strategy.
Furthermore, judges will be instructed to imagine that they win or lose money for every right or wrong prediction. I conjectured that including a money instruction would motivate judges to look at the "big picture" and therefore calculate a long-range payoff. Judges may infer that consistently choosing the more likely horse will yield net winnings instead of losses. In addition, Bereby-Myer and Erev (as cited in Erev et al., 1999) found that when losses are involved, judges perform better. Therefore, I predict that the money instruction will improve judges’ performance.
Method
Participants (judges) were asked to perform a two-choice probability learning task in which they made predictions in one of two scenarios. The scenario was either a horse race or an abstract event. Judges in the horse race condition were asked to predict the outcome of a series of horse races by clicking on Horse A or Horse B. In the abstract event condition, judges were asked to predict the occurrence of an event by clicking on R1 or R2. Each judge participated in one warm-up game and five experimental games of 100 races/trials each. After each game, judges were asked to judge their performance and the probabilities of events.
Instructions
Horse race scenario. Judges were instructed to try to predict which of two horses will win the next race by clicking on Horse A or Horse B. Three forms of instruction were manipulated: Strategy (strategy/no strategy), Money (money/no money), and Oddsmaker (oddsmaker/no oddsmaker). The Strategy instruction told judges to figure out which horse was better as soon as possible and always choose that horse. The Money instruction told judges to imagine winning or losing $100 for each race they predicted right or wrong. Finally, the Oddsmaker instruction presented an "oddsmaker" that advised judges what percentage of the time each horse should win a race. The oddsmaker instructions also advised judges to pay close attention to the oddsmaker’s opinion of the horses.
Abstract scenario. Two conditions used abstract events instead of horses, as in Birnbaum (in press). Judges were instructed to try to predict which value will occur next by clicking on R1 or R2 and were presented with the same additional instructions as in the horse race condition. However, the instructions were worded slightly different to reflect abstract events rather than horse races.
To view complete instructions, go to the following URL and click on the months:
http://psych.fullerton.edu/mbirnbaum/psych466/sw/Prob_Learn/
Design
The manipulated variables were the instructions presented to judges and the probability of events. Each instruction variable had two levels (instruction/no instruction). Thus, a 2 x 2 x 2, (Strategy x Money x Oddsmaker), between-subjects factorial design was used for the horse race scenario. In addition, a Content variable with two levels (horse race scenario/abstract scenario) was manipulated within the two extreme instruction conditions. The strategy/money/oddsmaker and the no strategy/no money/no oddsmaker instruction conditions were therefore presented with an abstract and a horse scenario. The other instruction conditions were only presented with the horse race scenario. Judges were assigned to 1 of the 10 instruction conditions according to their birth months, and the assignment to months was counterbalanced over the run of the study.
Each judge participated in five games of 100 trials each. For each game, the probability of an event was chosen randomly from the set 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, or 0.9. The probabilities were independent from game to game and subject to subject.
Materials and Procedure
The experiment consisted of a start-up page, warm-up page, and an experimental page. Judges entered the start-up page at the URL mentioned in the Instructions section. The start-up page had a brief description of the study and instructed judges to click on their birth month, which directed them to a warm-up page.
Each warm-up page was linked to its corresponding experimental page and represented 1 of the 10 instruction conditions. Each warm-up page contained an experimental panel (see Figure 1) and detailed instructions, which were displayed above the panel. In addition, an abbreviated version of the instructions appeared in an alert box when the judges pressed the "Start Warmup" button. The abbreviated instructions are displayed in Table 1. After playing a warm-up game of 100 races/trials, the judges saw three prompt boxes containing the following questions: (a) How many times (out of 100) did Horse B win (0 to 100)? (b) How many races (out of 100) did you get right? (c) If you had to predict on one race, which horse do you think would win? The wording was slightly different for the abstract scenario. After answering these questions, judges were directed to the experimental page by clicking on a link.
The experimental page contained the panel shown in Figure 1, except it did not have a "Start Warmup" button. Instead, an alert box automatically appeared as soon as a judge entered this page. The alert box contained the same abbreviated instructions presented in the warm-up trial. Judges participated in five games of 100 races/trials each. Following each game, judges were presented the same three judgment questions as in the warm-up game. After these questions were answered, an alert box with the same instructions appeared, which indicated the beginning of a new game. Although the instructions remained the same, the probability of events changed from game to game. When the five games were completed, participants saw a message that the experiment was finished and were directed to answer the items at the end of the page. These items included four demographic questions and one question that asked about judges’ gambling experience. The last item asked judges to explain their strategy for making predictions during the experiment. Results from experimental pages were sent through a JavaScript program to the CGI script that saved data on the server. The warm-up pages, however, did not send data.
Judges worked independently and were directed by instructions on the screen. The experiment could be completed in about 15 minutes, although each person worked at his or her own pace.
Participants
Participants were directed to the Web site by "sign-up" sheets at California State University, Fullerton or were recruited through the Web and by the experimenter. Out of 159 participants, approximately half were students who participated for class credit for an undergraduate psychology course.
Results
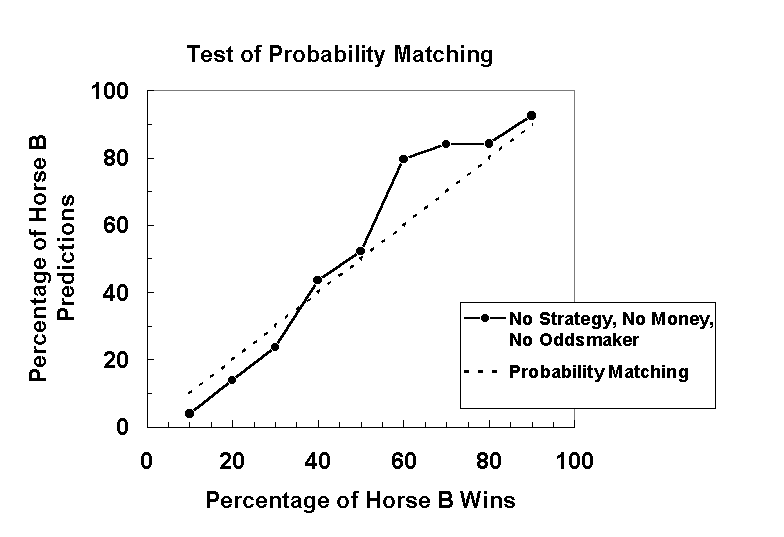
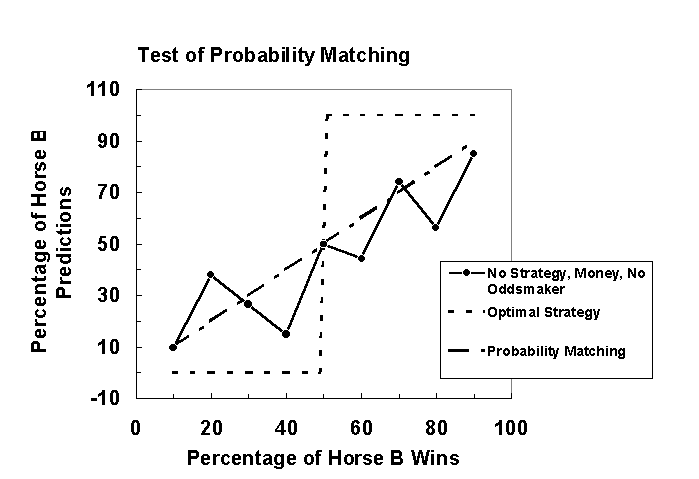
The dashed line in Figure 2 shows the probability matching strategy. The data points in this graph show the percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins in the no instruction condition. The data points fall close to the probability matching strategy line, which means that judges in this condition appeared to match probability of Horse B predictions to probability of Horse B wins. However, when Horse B won over 50% of the time, there was a slight improvement in performance, which is shown by the somewhat vertical alignment of the data points at 60%, 70%, and 80% wins.
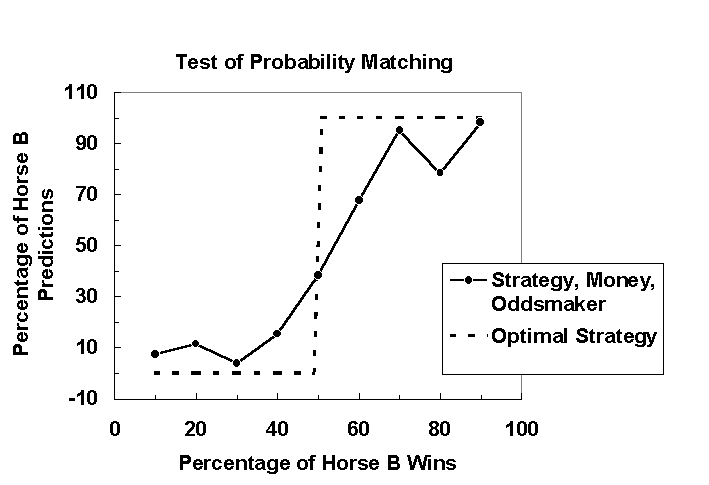
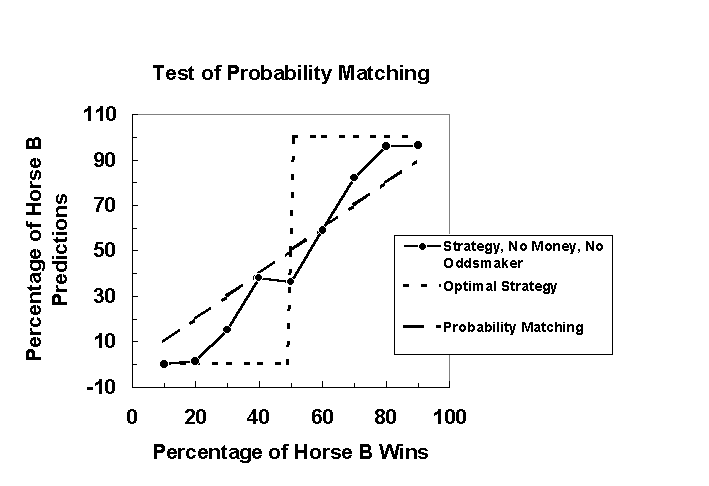
The dashed line in Figure 3 shows the optimal strategy, which is to always choose Horse A when the probability of Horse B winning is less than 50% and to always choose Horse B when its probability of winning is more than 50%. The data points in this graph represent the percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins when the strategy, money, and oddsmaker instructions were presented. When the probability of Horse B winning was less than 50%, judges chose Horse A over 80% of the time, which is close to optimal strategy. When Horse B won over 50% of the time, however, judges appeared to use the optimal strategy less often, especially at 60% and 80% wins. Although judges in this condition did not use the optimal strategy consistently, they did appear to probability match less than in the no instruction condition. Consequently, judges in this condition should have a higher percentage of correct predictions than in the no instruction condition. In fact, the percentage of correct predictions made in the strategy/money/oddsmaker was higher condition (M = 65.54) than in the no instruction condition (M = 63.82), indicating that judges used the optimal strategy more often when all three instructions were presented. These results were also found in Figure 4.
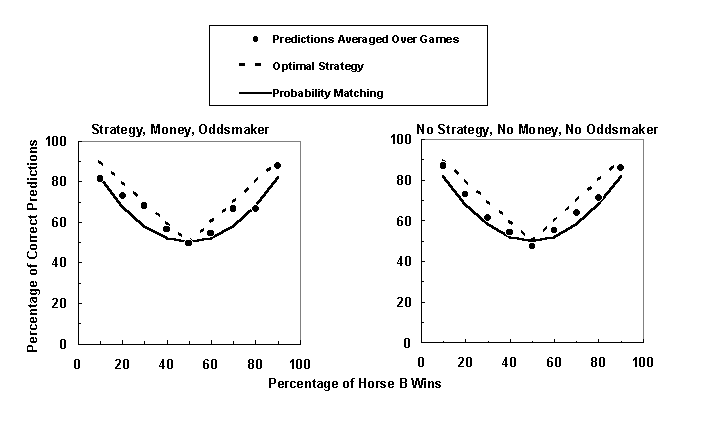
The dashed line in each graph in Figure 4 shows the optimal strategy, and the solid line shows the probability matching strategy. The right graph in the figure represents the no instruction condition, and the left graph represents the strategy/money/oddsmaker condition. The data points in these two graphs show the percentage of correct predictions averaged over five games as a function of percentage of Horse B wins. When comparing the two figures, it appears that more data points fall closer to the optimal strategy line in the strategy/money/oddsmaker condition than in the no instruction condition. Specifically, points at 30%, 40%, 70%, and 90% wins fall closer to the optimal strategy line in the strategy/money/oddsmaker condition, but only the point at 10% wins falls closer to the optimal strategy line in the no instruction condition. As predicted, judges that received the three instructions appeared to use the optimal strategy more often, and thus achieved a higher percentage of correct predictions than judges that did not receive instructions.
Table 2 displays the mean percentage of correct predictions for the strategy and no strategy conditions when oddsmaker and money instructions were and were not presented. This table shows that the highest percentage of correct predictions was achieved when judges were given the strategy instruction and not the oddsmaker and money instructions (M = 67.44). This table also shows that the lowest percentage of correct predictions was made when judges were presented with the money instruction and not the strategy and oddsmaker instructions (M = 58.76). These two conditions are shown in Figures 5 and 6.
The short-dashed line in Figures 5 and 6 shows the optimal strategy, and the long-dashed line shows the probability matching strategy. The graph in Figure 5 shows the percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins for the strategy/no money/no oddsmaker condition, which had the highest mean percentage correct. Data points in this graph show that judges in this instruction condition used the optimal strategy when the probability of Horse B winning was extreme (10%, 20%, 80%, and 90%), but were closer to probability matching when the probabilities were less extreme. The use of the optimal strategy at the probability extremes produced a high percentage of correct predictions, and therefore the performance in this condition appeared to be slightly better than in the strategy/money/oddsmaker condition.
The graph in Figure 6 shows the percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins for the no strategy/money/no oddsmaker condition, which had the lowest mean percentage correct. Data points in this graph show that judges in this condition did not use the optimal strategy. Instead, they appeared to either probability match or use some other suboptimal strategy, such as gambler’s fallacy, which leads to less correct predictions.
A 2 x 2 x 2 x 5 (Strategy x Oddsmaker x Money x Games) analysis of variance (ANOVA) was conducted to determine whether presenting instructions to judges improved their performance on the horse race probability learning task and if the instruction effects varied from game to game. No significant main effect was found for Strategy, Oddsmaker, Money, or Games. However, judges who were told the strategy to use achieved a higher percentage of correct predictions (M = 65.35) than judges not told the strategy (M = 63.15). Also, judges who were given probability of events (oddsmaker) had a higher percentage of correct predictions (M = 64.83) than judges not given probability of events (M = 63.82). Therefore, the strategy and oddsmaker instructions improved performance, although not significantly.
The money instruction was also hypothesized to improve performance; however, this was not supported by the data. Judges predicted a higher percentage correct when not given the money instruction. The mean percentage correct with money instruction was 63.68 and without was 64.83.
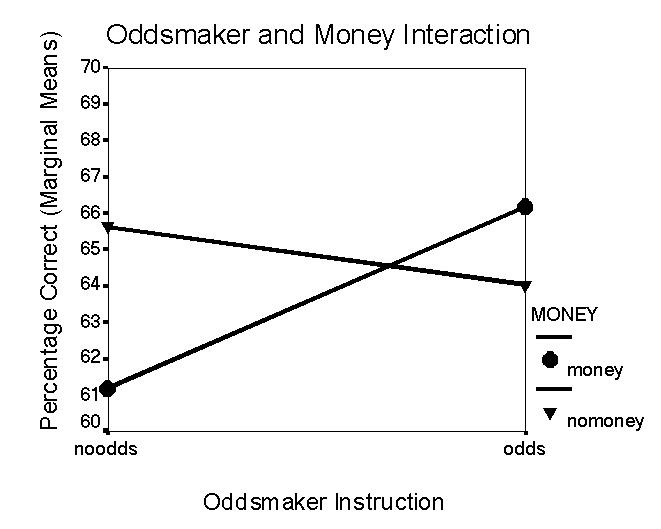
A significant interaction was found between money and oddsmaker instructions, F (1, 127) = 5.23, p < .05. Figure 7 shows the effects of the money instruction within each level of the oddsmaker instruction. The circles in the graph indicate judges were given the money instruction, and the triangles indicate that judges did not receive the money instruction. When the oddsmaker instruction was not presented, judges performed better without the money instruction than with the money instruction. The mean percentage of correct predictions when the oddsmaker and the money instructions were not presented was 65.63, and the mean percentage of correct predictions when the money instruction was presented without the oddsmaker instruction was 61.19.
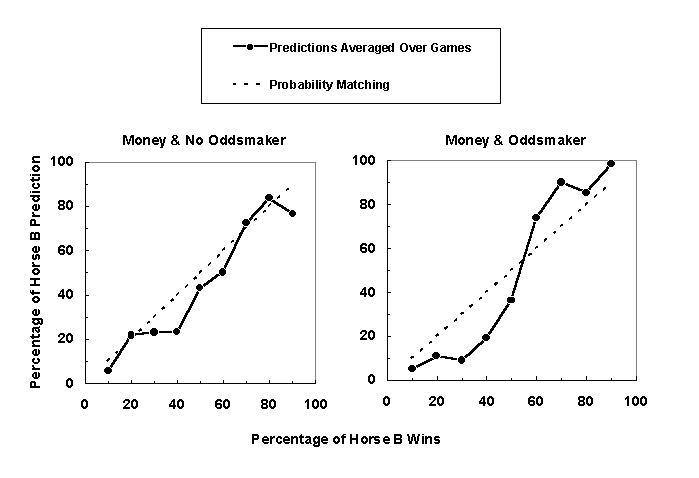
The graphs in Figure 8 show the percentage of Horse B predictions averaged over five games as a function of the percentage of Horse B wins. The left graph shows data points for the money/no oddsmaker condition, and the right graph shows data points for the money/oddsmaker condition. The dashed line in each graph shows the probability matching strategy. The strategy instruction was not considered in the graphs. A probability matching strategy is more salient in the money/no oddsmaker condition than in the money/oddsmaker condition. The stronger presence of the probability matching strategy in the money/no oddsmaker condition could explain the lower percentage of correct predictions in this condition.
It was predicted that the strategy and oddsmaker instructions presented together would lead to a higher percentage of correct predictions than the oddsmaker instruction presented alone. However, this was not supported by the data. Table 3 shows the mean percentage of correct predictions for the oddsmaker and no oddsmaker conditions when the strategy instruction was and was not presented. It appears that judges perform about the same when the oddsmaker instruction is presented with (M = 65.18) and without (M = 65.02) the strategy instruction. The worst performance was by judges who did not receive either instruction (M = 61.29).
Independent-sample t tests were performed to evaluate whether there was a significant difference between horse and abstract scenarios. Only one significant difference was found, which was in game 4 of the no instruction condition, t (33) = 2.47, p < .05. In game 4, judges who received the horse scenario achieved a higher percentage correct (M = 63.92) than judges who received the abstract scenario (M = 50.44). Overall, using a horse race scenario instead of an abstract scenario appeared to make a small difference in judges’ decision-making strategies, and therefore was not evaluated further.
Discussion
It was predicted that presenting judges with instructions would improve their performance in a two-choice probability learning task. Specifically, it was hypothesized that telling judges the optimal strategy and probability of events would shift their decision-making strategy from probability matching to optimal. It was also predicted that presenting judges with a money scenario in which they would win or lose money for every right or wrong prediction would lead them to think in terms of long-range payoffs. This in turn would help them realize that always choosing the more likely alternative would produce net winnings and is therefore the best strategy.
Although instructions used in this experiment produced a decline in the use of the probability matching strategy and an increase in the number of correct predictions, the instruction effects were not as strong as expected. In fact, the money instruction actually appeared to be detrimental to decision-making, in some cases. In addition, the horse race scenario and the abstract scenario produced similar results meaning that the context of the experiment did not affect judges’ decision-making strategies. Because of the small sample size within each condition, further investigation is needed for the results to be conclusive. Nevertheless, some reasons as to why these results were found are examined.
As in Nies’ (1962) research on a two-choice probability learning task, the present study found that telling judges probability of events increased the percentage of correct predictions. However, no significant effect was found for the oddsmaker instruction. In the Nies experiment, the "randomness" of events was made explicit to some judges. Nies speculated that the "randomness" aspect of his probability task (randomly mixed marbles in a box) prevented judges from inferring that marbles would roll out in some kind of pattern. When judges believe that sequence of events have a pattern, they tend to respond in this way, which leads to suboptimal decision-making strategies, including probability matching.
Perhaps judges in the present experiment did not perceive horse races as random events and therefore were inclined to look for patterns. In fact, when judges were asked what strategy was used during the experiment, several wrote they would start each game by looking for a pattern. Some also commented that "the pattern" was hard to find, which indicates that a pattern was assumed to exist.
Gal and Baron (1996) also found that judges do not necessarily choose the best strategy when the probability of events is given. Participants were asked to choose the best strategy for a binary learning task in which probability of events was known. Most of the participants responded that the "best" strategy is to choose the more likely event on "almost all" trials. Some participants who chose this strategy commented that when an event happens in a "streak", the other alternative is bound to happen, and one should switch to the other alternative after such a "streak" (i.e., gambler’s fallacy). Gal and Baron also found that when occurrences of events were scattered and not in "streaks", participants perceived the events as random and would be less likely to switch to the less likely alternative.
It appears that simply knowing probability of events does not necessarily lead to the use of the optimal strategy. A problem may be that people do not perceive events in probability learning tasks as independent of one another. This misconception could lead to gambler’s fallacy, pattern seeking, and probability matching. Explicitly telling participants that events are independent and random could therefore improve their performance on probability learning tasks.
Because people do not always know the best strategy to use, it was predicted that telling participants to always choose the more likely event, in addition to telling them the probability of events, would elevate the number of correct predictions. The data from this experiment did not support this hypothesis. The percentage of correct predictions did not increase significantly when the strategy instruction was presented with the oddsmaker instruction. Therefore, it appears that the misconceptions previously mentioned (gambler’s fallacy, pattern seeking, and probability matching) are not completely abandoned when the optimal strategy is given to judges.
An unexpected effect was found with the money instruction. Judges given this instruction had a slightly lower percentage of correct predictions than did judges not given this instruction. Furthermore, judges who were given the money and not the strategy and oddsmaker instructions had the smallest percentage of correct predictions.
The money instruction used in this experiment had a winning and losing component. Previous studies have found that losing money motivated people and led to more optimal decision-making strategies (Erev et al., 1999; Denes-Raj & Epstein, 1994). On the other hand, Arkes et al. (1986) found that judges who were not given incentives for correct judgments performed better than those who were offered incentives. It is theorized that when money (even if hypothetical) is at stake, people are less tolerant of wrong predictions and therefore are more likely to switch responses. Therefore, judges in this experiment that were presented the money instruction might have switched from the more likely horse to the least likely horse when a few incorrect predictions were made, especially when judges did not know the probability of events. Judges’ responses in relation to sequence of wins and losses were not recorded in this experiment. Therefore, this conjecture was not verifiable. Nevertheless, it appears that sequence of events influences judges’ decision-making.
Chau et al. (2000) also found that sequence of events was important, especially for the first few trials. People that were told the "best" strategy to use during a game of blackjack were less likely to follow the strategy if they lost on the first few trials. Some judges in the present study also appeared to base their choices on the first few trials. One judge commented that he "stuck to the first winner", and a couple of people wrote that they based their predictions on the first few trials. Therefore, sequence of events, especially for the first few trials, could affect judges’ responses to instructions. Future studies should examine this possibility.
Future studies on probability learning should also examine the effect of feedback that judges’ receive. Arkes et al. (1986) found that when judges were not given feedback their performance improved because they were not receiving the negative feedback that often leads to the use of a suboptimal strategy.
Assuming that people want to maximize their success, they should use available information to achieve this end. However, the problem appears to be that people do not know how to use the potentially helpful information in a probability learning task. Future studies are needed to further investigate this problem.
References
Arkes, H. R., & Dawes, R. M. (1986). Factors influencing the use of a decision rule in a probabilistic task. Organizational Behavior and Human Decision Processes, 37, 93-110.
Birnbaum, M. H. (in press). Wahrscheinlickkeitslernen (probability learning). In D. Janetzko, H. A. Meyer, & M. Hildebrand (Eds.), Das expraktikum im labor und WWW [A practical course on psychological experimenting in the laboratory and in the WWW]. Gottingen, Germany: Hogrefe.
Brehmer, B., & Kuylenstierna, J. (1980). Content and consistency in probabilistic inference tasks. Organizational Behavior and Human Performance, 26, 54-64.
Chau, A. W. L., Phillips, J. G., & Von Baggo, K. L. (2000). Departures from sensible play in computer blackjack. The Journal of General Psychology, 127, 426-438.
Denes-Raj, V., & Epstein, S. (1994). Conflict between intuitive and rational processing: When people behave against their better judgment. Journal of Personality and Social Psychology, 66 (5), 819-829.
Erev, I., Bereby-Meyer, Y., & Roth, A. E., (1999). The effect of adding a constant to all payoffs: Experimental investigation, and implication for reinforcement learning models. Journal of Economic Behavior & Organization, 39, 111-128.
Gal, I., & Baron, J. (1996). Understanding repeated simple choices. Thinking and Reasoning, 2 (1), 81-98.
Herrnstein, R. J. (1990). Behavior, reinforcement and utility. Psychological Science, 1 (4), 217-224.
Nies, R. C. (1962). Effects of probable outcome information on two-choice learning. Journal of Experimental Psychology, 64 (5), 430-433.
Tversky, A. & Edwards, W. (1966). Information versus reward in binary choices. Journal of Experimental Psychology, 71 (5), 680-683.
Footnotes
1I would like to thank Michael H. Birnbaum for his help in creating the Web pages for this experiment and his assistance in the analysis and design. Also, thanks to the students of Psychology 466 for their preliminary testing of the experiment and their valuable input.

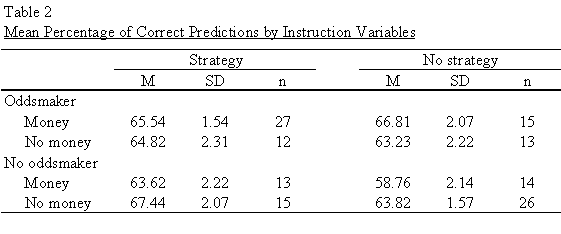

Figure Captions
Figure 1. Experimental panel in warm-up page. Judges made predictions by clicking on Horse A or Horse B. The box above the correct answer choice displayed the correct event, and the panel in the center told judges whether they were "Right" or "Wrong" for 220 ms. In the abstract task conditions, "R1" and "R2" replaced "Horse A" and "Horse B".
Figure 2. Percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins in the no strategy/no money/no oddsmaker condition. Data points in this condition fall close to the probability matching line (dashed-line) indicating that judges had a tendency to use the probability matching strategy.
Figure 3. Percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins in the strategy/money/oddsmaker condition. Data points fall close to the optimal strategy line (dashed-line) indicating that judges in this condition had a tendency to use the optimal strategy of always choosing the more likely horse, although some points fall close to the probability matching strategy.
Figure 4. Percentage of correct Horse B predictions averaged over five games as a function of percentage of Horse B wins. The left graph is for the strategy/money/oddsmaker condition, and the right graph is for the no instruction condition. The dashed line in each graph shows the optimal strategy, and the solid line shows the probability matching strategy. More data points in the strategy/money/oddsmaker condition fall closer to the optimal strategy line than in the no instruction condition.
Figure 5. Percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins in the strategy/no money/no odds condition. Short-dashed lines and long-dashed lines in the graph show optimal strategy and probability matching predictions, respectively. Data points show that judges had a tendency of using the optimal strategy when the probabilities of Horse B winning were extreme.
Figure 6. Percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins in the no strategy/money/no oddsmaker condition. Short-dashed lines and long-dashed lines in the graph show optimal strategy and probability matching predictions, respectively. Data point show that judges in this condition did not use the optimal strategy.
Figure 7. Effect of money instruction within oddsmaker instruction. A significant interaction was found between these two instruction variables. Money instruction improved performance when presented with the oddsmaker instruction; however, it did not improve performance when presented without the oddsmaker instruction.
Figure 8. Percentage of Horse B predictions averaged over five games as a function of percentage of Horse B wins. The left graph shows data points for the money/no oddsmaker condition, and the right graph shows data points for the money/oddsmaker condition. The dashed line shows the probability matching strategy.