Homework No 4: H and C

Homework No. 4: H and C
Outline of Psychological Measurement

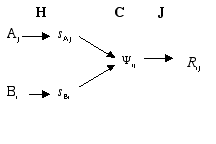
Response = J[C(H(A), H(B))]

A_j and B_i are the stimuli for Column j and Row i.

s_{A_j} and s_{B_i} are the subjective, scale values for the stimuli.

Y_ij is the subjective impression of the combination of A_j and B_i.

R_ij is the overt response to this combination.

H are the functions that assign subjective values to the stimuli.

C is the combination function combining the subjective values.

J is the judgment function that assigns responses to impressions.

In this assignment, we let J be the identity function; i.e., R_ij = Y_ij

Homework:

Make predictions for a 4 x 4, A x B, symmetric, factorial design using integers from 1 to 4 for levels of A and B. (s_{A_j} = A_j = j; s_{B_i} = B_i = i). Plot predictions as a function of A with a separate curve for each level of B.

Part A: H and J are identity functions.

1. Additive: T_ij = s_{A_j} + s_{B_i}

2. Multiplicative: P_ij = s_{A_j} s_{B_i}

3. Subtractive: D_ij = s_{A_j} - s_{B_i}

4. Ratio: R_ij = s_{A_j}/s_{B_i}

Part B: Repeat Part A, but now let H be a power function (square):

s_{A_j} = H(A_j) = A² Similarly, let s_{B_i} = H(B_i) = B²

Part C: Repeat Part A, but substitute A^.5 and B^.5 for H(A) and H(B)

(H(B) = square root of B).

Part D: Repeat Part A, substituting log(A+1) and log(B+1) for H(A) and H(B).

Part E: What remains the same, irrespective of H, for the additive model? What changes? How can you use these graphical properties to separate H and C? Given a new set of data, how would you decide what model is appropriate? How would you determine H? Before you answer this question, organize your sixteen graphs for Parts A through D and additive, multiplicative, subtractive, and ratio models.

Return to the Index